Finding Closest Geographical Points: A Comparative Approach

Data Science
1

:earth_africa: 𝐅𝐒𝐧𝐝𝐒𝐧𝐠 𝐂π₯𝐨𝐬𝐞𝐬𝐭 π†πžπ¨π π«πšπ©π‘π’πœπšπ₯ 𝐏𝐨𝐒𝐧𝐭𝐬: 𝐀 π‚π¨π¦π©πšπ«πšπ­π’π―πž π€π©π©π«π¨πšπœπ‘

In the world of data science and geospatial analysis, identifying the closest points between datasets is a common yet crucial task. Recently, I explored two different methodologies to achieve this objective using Python.

:one: π‘ͺπ’‚π’“π’•π’†π’”π’Šπ’‚π’ 𝑷𝒓𝒐𝒅𝒖𝒄𝒕 𝒂𝒏𝒅 π‘―π’‚π’—π’†π’“π’”π’Šπ’π’† π‘­π’π’“π’Žπ’–π’π’‚

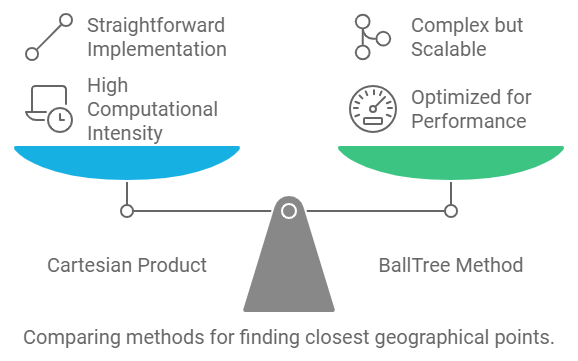
The first approach involves calculating the Cartesian product of two datasets and applying the Haversine formula to determine distances. While this method is straightforward, it can be computationally intensive for larger datasets.
:open_file_folder: Check out the code here: Python_For_RF_Optimization_And_Planning_Engineer/Distance/Calculate_Min_Distance_Using_haversine.md at main Β· Umersaeed81/Python_For_RF_Optimization_And_Planning_Engineer Β· GitHub

:two: π‘¬π’‡π’‡π’Šπ’„π’Šπ’†π’π’• 𝑡𝒆𝒂𝒓𝒆𝒔𝒕 π‘΅π’†π’Šπ’ˆπ’‰π’ƒπ’π’“ 𝑺𝒆𝒂𝒓𝒄𝒉 π’˜π’Šπ’•π’‰ 𝑩𝒂𝒍𝒍𝑻𝒓𝒆𝒆

The second approach leverages the BallTree data structure for a more efficient nearest neighbor search. This method is optimized for performance, especially when working with larger datasets, making it a more scalable solution.
:open_file_folder: Check out the code here: Python_For_RF_Optimization_And_Planning_Engineer/Distance/Calculate_Min_Distance_Using_sklearn.md at main Β· Umersaeed81/Python_For_RF_Optimization_And_Planning_Engineer Β· GitHub

Both methods ultimately aim to identify the closest geographical points, but they differ significantly in their performance and complexity. I encourage fellow data enthusiasts to take a look and consider which approach best suits their needs!

Feel free to share your thoughts and experiences in the comments below!
min_distance_linedin